The Arcball or Trackball is an elegant and intuitive input method to rotate and manipulate a three-dimensional scene with the mouse. The idea behind was proposed by Ken Shoemake [Shoemake] and is quite easy to understand and to implement which led to the fact that today it is actually the primary mechanism that people use to rotate objects in 3D computer environments.
The Arcball tackles the problem that the mouse is in 2D and the object is in 3D by picturing a sphere behind the screen that when clicked pinches the sphere and by dragging, the sphere is rotated around its center with all its associated objects. In this WYSIWYG way, the scene rotates in a direction that intuitively corresponds to the direction in which we move the mouse. It feels even more naturally when used on a touch screen.
With Trackball.js it is easy to implement a virtual Trackball right with HTML5 and CSS3.
Mathematical Derivation of an Arcball
Transform mouse coordinates to canonical space
Let the cursor position \(P\) be in the viewport space, typically in the x-y plane:
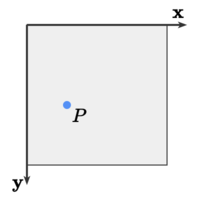
Now convert the screen coordinates (in pixels) to the canonical space by scaling down the mouse coordinate from the range of \([0\dots\text{width})\), \([0\dots\text{height}\)) to \([-1...1]\), \([1...-1]\).
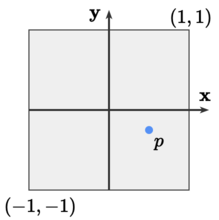
To do so, we subtract the screen center \(C = \frac{1}{2}(\text{width} - 1, \text{height} - 1)\), divide the result by the smallest scale \(s=\min(\text{width}, \text{height}) - 1\) to get the largest circle in the viewport (or individually divide by \(\text{width} - 1\) and \(\text{height} - 1\) to get an ellipse). The scaled down point (lower case) \(p\) is thus
\[\begin{array}{rl} p_x &= +\frac{2}{s}(P_x - C_x) = +\frac{1}{s}(2P_x - \text{width} + 1)\\ p_y &= -\frac{2}{s}(P_y - C_y) = -\frac{1}{s}(2P_y - \text{height} + 1) \end{array}\]
Project the position to a hemi-sphere
The first step of generating an Trackball consists of defining the ball itself, which is a sphere at the origin:
\[x^2 + y^2 + z^2 = r^2\]
The idea now is, that we use our mouse position as the projection of a point on a hemi-sphere, which takes the given point \(p\) and a radius \(r\in(0, 1]\) (typically 1) to calculate the depth:
\[z(p_x, p_y) = \sqrt{r^2 - p_x^2 - p_y^2}\]
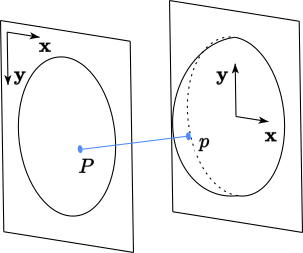
We now use the canonical point \(p\) and the depth information on the sphere \(z(p_x, p_y)\) to form a three dimensional vector from the origin \(\mathcal{O}=(0,0,0)\):
\[\mathbf{p} = (p_x, p_y, z(p_x, p_y))\]
Fixing points outside the hemi-sphere
When points outside the radius of the sphere get clicked, \(z\) becomes complex as we have a negative square root. Typically, people set \(z(p_x, p_y)=0\) when \(p_x^2 + p_y^2 > r^2\), which was also proposed in the original paper. They see it as a feature to rotate around the axis, but it feels more like a bug.
A better idea is to use a piecewise combination of functions instead of relying on the sphere alone. One function that is often used in conjunction with the original \(z(p_x, p_y)\) is the hyperbolic function
\[f(x, y) = \frac{r^2/2}{\sqrt{x^2 + y^2}}\]
\(f\) and \(z\) intersect on the circle with radius \(\frac{r^2}{2}\). When combining the individual functions we get a smooth corrected z-coordniate:
\[z(x, y) = \begin{cases} \sqrt{r^2 - x^2 - y^2} &\text{if } x^2 + y^2\leq r^2/2 \\ \frac{r^2/2}{\sqrt{x^2 + y^2}} &\text{else } \end{cases}\]
When you imagine the normal of the surface, it is clear that the handling gets unstable the closer you get to the radius of the ball. Using the corrected function is much smoother in that regard:

Handling mouse motion on the hemi-sphere
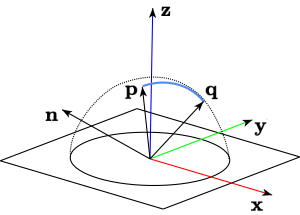
Suppose we have our derived mouse-down vector \(\mathbf{p}\) on the hemi-sphere. Now for each mouse-move event, we can calculate a second vector \(\mathbf{q}\) in the same way to map each updated position on the hemi-sphere until we release the mouse button.
To create a great arc, which is the shortest path from one point to another on a sphere, we calculate the cross product of both vectors \(\mathbf{p}\) and \(\mathbf{q}\) to get the rotation axis (orthogonal to both vectors). Remember that every arc lies in the plane perpendicular to its rotation axis.
The angle \(\theta\) between the two vectors \(\mathbf{p}\) and \(\mathbf{q}\) comes also naturally by the dot product.
\[\begin{array}{rl} \theta &= \cos^{-1}\left(\frac{\mathbf{p}\cdot\mathbf{q}}{|\mathbf{p}||\mathbf{q}|}\right)\\ \mathbf{n} &= \mathbf{p}\times\mathbf{q} \end{array}\]
Note that \(|\mathbf{p}|=|\mathbf{q}|=1\) is only true on the ball when we chose \(r=1\)! As soon as we enter the correction hyperbolic function, the length varies. The same applies for \(\mathbf{n}\), which does not have a unit length, even if \(\mathbf{p}\) and \(\mathbf{q}\) are normalized!
Using Quaternions as representation
A quaternion is a much more elegant way to represent rotations in space than rotation matrices. Intuitively, a (normalized) quaternion in the axis-angle interpretation is a directional vector and the rotation angle around this vector. In this way every rotation in three dimensions is possible by four numbers, the vector \(\mathbf{n}=(x,y,z)\) and a fourth number \(w\). A unit quaternion (versor) \(\mathbf{Q}\) then describes a rotation with
\[\mathbf{Q} = \left(\cos\frac{\theta}{2}, \sin\frac{\theta}{2}\hat{\mathbf{n}}\right)\]
We have \(\sin\) and \(\cos\) in this equation, but typically they cancel out so that rotations can be computed much faster with only multiplications and additions! A rotation is simply a quaternion multiplication instead of a matrix-matrix multiplication:
\[\mathbf{Q_1\times Q_2} := (w_1w_2 - \mathbf{n_1}\cdot \mathbf{n_2}, w_1\mathbf{n_2} + w_2\mathbf{n_1}+\mathbf{n_1}\times\mathbf{n_2})\]
\(\mathbf{n_1}\times\mathbf{n_2}\) here is the 3D vector cross product, which is the reason that quaternion multiplication is not commutative!
The inverse rotation \(\mathbf{Q}^{-1}\) is equal to the conjugate \(\overline{\mathbf{Q}}\), which is flipping over the imaginary part:
\[\overline{\mathbf{Q}}:= (w, -\mathbf{n})\]
The last step that is necessary to do with our quaternion is to apply it to all objects the Trackball controls. To do so, we embed our vector \(\mathbf{v}\) we want to rotate into a quaternion and rotate it with two quaternion multiplications:
\[Rot(\mathbf{v}):= \mathbf{Q}\times(0, \mathbf{v})\times\overline{\mathbf{Q}}\]
Multiplying two times is only necessary in theory, as rotating vectors using quaternions can be optimized a lot. Did I mention, quaternions don't have the problem of gimbal locks! Is there a reason to use rotation matrices or Euler angles ever again? Especially when libraries like Quaternion.js do all the heavy work for you ;-)
Summary
\[\begin{array}{rl} z(x, y) &= \begin{cases} \sqrt{r^2 - x^2 - y^2} &\text{if } x^2 + y^2\leq r^2/2 \\ \frac{r^2/2}{\sqrt{x^2 + y^2}} &\text{else }\\ \end{cases}\\ \mathbf{p} &= (p_x, p_y, z(p_x, p_y))\\ \mathbf{q} &= (q_x, q_y, z(q_x, q_y))\\ \theta &= \cos^{-1}\left(\hat{\mathbf{p}}\cdot\hat{\mathbf{q}}\right)\\ \mathbf{n} &= \mathbf{p}\times\mathbf{q}\\ \mathbf{Q} &= \left(\cos\frac{\theta}{2}, \sin\frac{\theta}{2}\hat{\mathbf{n}}\right) \end{array}\]
Where \(\hat{\mathbf{v}}:= \frac{\mathbf{v}}{|\mathbf{v}|}\) is the normalized vector of \(\mathbf{v}\). Good quaternion libraries probably ship a function like fromBetweenVectors to go directly from \(\mathbf{p}\) to \(\mathbf{q}\) via a quaternion \(\mathbf{Q}\), as it is possible to optimize this step tremendously.
Implementation scheme
function init() {
lastQ = Quaternion.ONE // Initial orientation
currQ = Quaternion.ONE // Identity
start = null
}
function mousedown(x, y) {
start = { x, y }
}
function mousemove(x, y) {
if (start == null) return
a = project(start.x, start.y)
b = project(x, y)
currQ = Quaternion.fromBetweenVectors(a, b)
}
function mouseup(x, y) {
if (start == null) return
lastQ = currQ.mul(lastQ)
currQ = Quaternion.ONE
start = null
}
function project(x, y) {
radius = 1
res = min(width, height) - 1;
// map to -1 to 1
x = (2 * x - width - 1) / res
y = (2 * y - height - 1) / res
d = x * x + y * y
if (2 * d <= r * r)
z = sqrt(r * r - d);
else
z = r * r / 2 / sqrt(d);
return [x, y, z]
}
function draw() { // Repeated drawing function
rotation = currQ.mul(lastQ)
rotated = rotation.rotateVector(object)
}
References
- ShoemakeKen Shoemake (1992) ARCBALL: A User Interface for Specifying Three-Dimensional Orientation Using a Mouse
- HenriksenKnud Henriksen (2004) Virtual Trackballs Revisited