Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
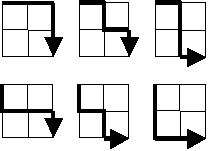
How many such routes are there through a 20×20 grid?
Solution
This is a problem which can be solved with dynamic programming quite easily. If we had a 1x1 grid, we would have only 2 possibilities to get to the solution. As given in the problem statement, with a 2x2 grid, we have 6 ways to get to the solution, which is the previous two ways plus one additional way in each direction: \((2+1)\cdot 2\). We can abstract on this and say, the sum of the previous element on the left and top gives the new desired sum. Building a table with this principle gives the result in the bottom right cell. Implemented, this looks like:
function solution(size) {
var dp = new Array(size + 1);
for (var i = 0; i <= size; i++) {
dp[i] = new Array(size + 1).fill(0);
}
dp[0][0] = 1;
for (var i = 0; i <= size; i++) {
for (var j = 0; j <= size; j++) {
if (i) dp[i][j]+= dp[i-1][j];
if (j) dp[i][j]+= dp[i][j-1];
}
}
return dp[size][size];
} This solution is quite memory dissipating, but since the resulting table is symmetric, we could strip off some bytes. A better way however would be to understand the generating principle of the diagonal, which follows the series \(1, 2, 6, 20, 70, 252, 924, ...\) A quick look at oeis.org gives us the solution. However, let's try to understand what's going on.
What we really generated with the table is Pascal's triangle and we're interested in all the middle elements, which are the diagonal elements in our dynamic programming table. Every element of the triangle can be calculated with the binomial coefficient and every desired element for our problem can be calculated with \(\left(\begin{array}{cc}2n\\ n \end{array}\right)\). This is the same as we could have looked up based on the series.
That's really interesting! That actually expresses a combinatoric relationship. So let's try to figure out what that means from that point of view. What we can do in each cell is going down (D) or right (R). For the 1x1 example this is \((R,D)\) and \((D,R)\). For the 2x2 example, it is \((R,R,D,D), (R,D,R,D), (R,D,D,R), (D,R,R,D), (D,R,D,R), (D,D,R,R)\). The number of elements of these sets is \(2n\) and we have \(n\) elements we want to arrange under this length, which results in the same equation!
Now to the implementation part. I wrote a highly optimized n over k function for my MySQL UDF, which utilizes symmetry and is bound to \(O(k)\). Implemented in JavaScript, this looks like:
function noverk(n, k) {
if (n < k || k < 0)
return 0;
k = Math.min(k, n - k);
n = n - k;
for (var i = 1, c = 1; i <= k; i++)
c = c * (n + i) / i;
return c;
} But since we have a binomial coefficient dependent only on \(n\), we can simplify the function even further for our problem:
function solution(n) {
for (var i = 1, c = 1; i <= n; i++)
c = c * (n + i) / i;
return c;
}
solution(20); All images are copyright to Codingame